Standardabweichung, or standard deviation, is a term you might have come across in statistics class or while analyzing data. But what does it really mean? Why should you care about it? Whether you’re a student trying to ace your math exams, a business analyst interpreting market trends, or simply curious about how data can tell us more than just numbers on a page, understanding standardabweichung is essential.
This measure of variability provides insights into how much individual values differ from the average. It helps make sense of everything from test scores to financial reports and even everyday decisions. Ready to dive deep into this statistical tool? Let’s break down the steps for calculating standardabweichung effectively. You’ll be equipped with knowledge that not only enhances your analytical skills but also empowers your decision-making processes in various aspects of life!
Understanding Standardabweichung
Standardabweichung, or standard deviation, is a statistical measure that quantifies the amount of variation or dispersion in a set of values. Essentially, it tells you how spread out the numbers are around the mean.
When most values cluster closely to the average, you have a low standardabweichung. Conversely, if they are widely varied from one another and from the mean, this results in a higher value.
Understanding this concept is key for interpreting data effectively. It helps analyze trends and patterns across various fields—be it finance, education, or scientific research.
For example, in finance, investors use standardabweichung to gauge market volatility. In educational settings, teachers can assess student performance variability with this tool. Grasping its significance allows for deeper insights into any dataset you’re working with.
Why is Standardabweichung Important?
Standardabweichung, or standard deviation, plays a crucial role in data analysis across various fields. It provides insight into the variability of data points within a dataset. Understanding this variability helps researchers and analysts make more informed decisions.
In finance, for instance, standardabweichung is used to assess risk. A higher deviation indicates greater volatility in stock prices, guiding investors on potential risks associated with their portfolios.
In scientific research, it aids in interpreting experimental results. By knowing how much individual observations differ from the mean, scientists can determine whether their findings are significant.
Moreover, standardabweichung enhances quality control processes in manufacturing. Companies rely on it to ensure products meet consistent standards by examining variations during production runs.
Grasping the concept of standardabwweichung allows professionals to better understand trends and patterns within their data-driven projects.
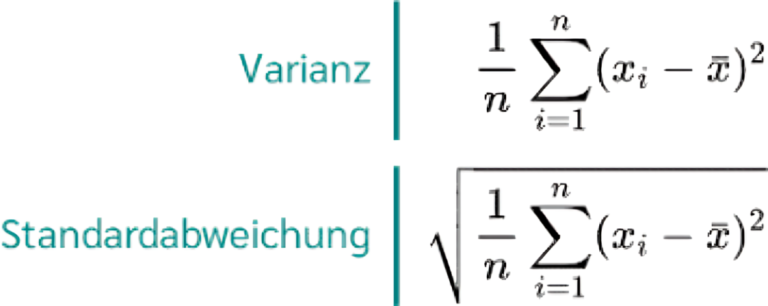
The Formula for Calculating Standardabweichung
To calculate the Standardabweichung, or standard deviation, you need a clear formula. It helps quantify how spread out numbers are in your dataset.
The basic formula for Standardabweichung is:
σ = √(Σ(xi – μ)² / N)
Here, σ represents the population standard deviation. The symbol Σ indicates that you will sum up all values.
In this case, xi stands for each individual data point. Meanwhile, μ is the mean of those points. You subtract the mean from each data point and square it to eliminate negative values.
Divide by N—the total number of observations—before taking the square root to get your final result. This method gives you valuable insight into variability within your dataset. Understanding this formula lays the groundwork for further statistical analysis and interpretation.
Step-by-Step Instructions for Calculating Standardabweichung
Calculating Standardabweichung is straightforward when you break it down into manageable steps. Start by gathering your data set. This could be anything from test scores to daily temperatures.
Next, find the mean of your data. Add all the values together and divide by the number of entries. This gives you a central reference point.
Then, subtract the mean from each data point to determine deviations. Square each deviation for accuracy—this prevents negative values from skewing results.
Add up all those squared deviations next.
Now, take that sum and divide it by the total number of observations if you’re calculating population standardabweichung or by one less than that count for sample standardabweichung.
Take the square root of this quotient. What you have now is your Standardabweichung! Each step builds on the last, making it easier to understand as you go along.
Example Calculation using Real Data
Let’s dive into an example to calculate the Standardabweichung using real data. Imagine you have a small dataset representing the ages of five friends: 22, 25, 27, 30, and 31.
First, find the mean (average) age. Add all ages together: \(22 + 25 + 27 + 30 + 31 = 135\). Then divide by the number of friends: \(135 / 5 = 27\).
Next, subtract the mean from each age to find deviations:
– For age \(22\): \(22 – 27 = -5\)
– For age \(25\): \(25 – 27 = -2\)
– For age \(27\): \(0\)
– For age \(30\): \(3\)
– For age \(31\): \(4\)
Square these deviations:
– \((-5)^2 = 25,\)
– \((-2)^2 = 4,\)
– \((0)^2 =0,\)
– \((3)^2=9,\)
– \((4)^2=16.\)
Now add them up:
\(25 +4+0+9+16=54.\)
To get variance, divide by your sample size minus one (\(n –1=4)\):
\(54/4=13.5.\)
Take the square root of variance for Standardabweichung:
√13.5 ≈ **3.67**.
Common Mistakes to Avoid when Calculating Standardabweichung
When calculating Standardabweichung, one common mistake is using the wrong formula. Ensure you’re clear on whether you need to calculate the population or sample standard deviation. These formulas differ slightly.
Another frequent error is not properly handling negative values. Remember, squaring your deviations will eliminate negatives, but be cautious with interpretations afterward.
Failing to double-check your data set can lead to incorrect results as well. Even a single misplaced number can skew your calculations significantly.
Many overlook rounding procedures too soon in their calculations. Always maintain precision until the final step for more accurate results.
Remember that context matters. Misinterpreting what the standard deviation indicates about your data can lead to misguided conclusions about variability and trends in your research or analysis.
Practical Applications of Standardabweichung
Standardabweichung, or standard deviation, plays a vital role in various fields. It’s not just a mathematical concept; it’s a practical tool used across industries.
In finance, investors rely on standardabweichung to assess the volatility of their portfolios. A higher value indicates greater risk and potential return, guiding informed investment decisions.
In healthcare, researchers use it to analyze patient data. Understanding variations in clinical trial results helps determine treatment effectiveness and safety profiles.
Education benefits from this metric as well. Teachers can evaluate test scores and identify learning gaps among students. This insight fosters tailored teaching strategies for better outcomes.
Manufacturing relies on standardabweichung to monitor product quality. By measuring variation in production processes, companies can maintain consistency and reduce defects.
From sports analytics to marketing research, the applications are endless. Standardabweichung provides clarity amidst complexity, making it an indispensable part of data analysis across diverse sectors.
FAQs
What is the difference between Standardabweichung and Varianz?
Standardabweichung measures the dispersion of data points from their mean. Varianz, or variance, calculates how much each number in a dataset varies from the average squared. While related, they serve different purposes.
How does sample size affect Standardabweichung?
A larger sample size generally provides a more accurate representation of the population. This can lead to a more reliable calculation of Standardabweichung.
Can I calculate Standardabweichung using Excel?
Absolutely! Excel has built-in functions like STDEV.
P for populations and STDEV.
S for samples. These tools simplify calculations significantly.
Why is it important to understand Standardabweichung?
Understanding this concept helps interpret data variability effectively, guiding better decision-making across various fields such as finance or research.
Conclusion
Understanding and calculating the standardabweichung can be quite beneficial across various fields, from finance to education. By mastering this essential statistical concept, you empower yourself to make informed decisions based on data analysis.
The steps outlined in this guide provide a clear path for anyone looking to understand or calculate the standardabweichung accurately. With practice, you’ll find that it becomes second nature.
Remember that avoiding common pitfalls during your calculations is crucial. This awareness will help ensure your results are both reliable and insightful.
As you apply your knowledge of standardabweichung in real-world scenarios, whether you’re evaluating business performance or analyzing test scores, you’ll recognize its value as a tool for understanding variability within your data sets. The clearer grasp you have on this measure of dispersion, the more adept you’ll become at interpreting information critically.
Continue exploring and applying these concepts; they hold significant potential for enhancing analytical skills and decision-making abilities over time. Your journey into statistics has just begun!